In computer science, a binary tree is a k-ary, �=2k=2 tree data structure in which each node has at most two children, which are referred to as the left child and the right child. A recursive definition using just set theory notions is that a (non-empty) binary tree is a tuple (L, S, R), where L and R are binary trees or the empty set and S is a singleton set containing the root. Some authors allow the binary tree to be the empty set as well.

binary tree representation

Definitions

The highest node in a binary tree is known as the root, and the base most nodes are called leaves. A twofold tree can be envisioned as a various leveled structure with the root at the top and the leaves at the base

binary tree have numerous applications in software engineering, including information stockpiling and retrival, articulation assessment, network steering, and game simulated intelligence. They can likewise be utilized to embed different calculations, for example, looking, arranging, and chart arrangements

To characterize a binary tree, the likelihood that only one of the youngsters might be unfilled should be recognized. A curio, which in certain course readings is called a drawn out parallel tree, is required for that reason. A lengthy binary tree is along these lines recursively characterized as:

• the vacant set is a lengthy paired tree

• in the event that T1 and T2 are expanded parallel trees, mean by T1 • T2 the drawn out twofold tree got by adding a root r associated with the left to T1 and to the right to T2[clarification required where did the 'r' go in the 'T1 • T2' symbol] by adding edges when these sub-trees are non-void.

One more approach to envisioning this development (and grasping the wording) is to consider rather than the vacant set an alternate kind of node — for example square nodes in the event that the customary ones are circles.

Properties of a binary tree

· The maximum number of nodes at level ‘l’ of a binary tree is 2^l

· The maximum number of nodes in a binary tree of height ‘h’ is (2^h)-1

· In a binary tree with N nodes, the maximum possible height or maximum number of levels is log(N+1)

· A binary tree with L leaves has at least has at least | log l|+1 levels

· In a binary tree where every node has 0 or 2 children, the number of leaf nodes is always one more than nodes with two children

· In a non-empty binary tree if n is the total number of nodes and e is the total number of edges then e=n-1

Types of binary trees

· A rooted binary tree has a root node and every node has at most two children.

· A full binary tree (sometimes referred to as a proper^] or plane or strict binary tree) is a tree in which every node has either 0 or 2 children. Another way of defining a full binary tree is a recursive definition. A full binary tree is either:

o A single vertex.

o A tree whose root node has two subtrees, both of which are full binary trees.

· A perfect binary tree is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level.^]An example of a perfect binary tree is the ancestry chart of a person to a given depth less than that at which an ancestor would appear more than once in the chart (at which point the chart is no longer a tree with unique nodes; note that the same ancestor can appear at different depths in the chart), as each person has exactly two biological parents (one mother and one father). Provided the ancestry chart always displays the mother and the father on the same side for a given node, their sex can be seen as an analogy of left and right children, children being understood here as an algorithmic term.

· A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2^h nodes at the last level h. A perfect tree is therefore always complete but a complete tree is not necessarily perfect. An alternative definition is a perfect tree whose rightmost leaves (perhaps all) have been removed. Some authors use the term complete to refer instead to a perfect binary tree as defined above, in which case they call this type of tree (with a possibly not filled last level) an almost complete binary tree or nearly complete binary tree. A complete binary tree can be efficiently represented using an array.

· the infinite complete binary tree is a tree with N0 levels, where for each level d the number of existing nodes at level d is equal to 2^d. The cardinal number of the set of all levels is N0 (countably infinite). The cardinal number of the set of all nodes (or paths) is uncountable, having the cardinality of the continuum.

· A balanced binary tree is a binary tree structure in which the left and right subtrees of every node differ in height by no more than 1. One may also consider binary trees where no leaf is much farther away from the root than any other leaf. (Different balancing schemes allow different definitions of "much farther".)

A degenerate (or pathological) tree is where each parent node has only one associated child node. This means that the tree will behave like a linked list data structure

Application of binary tree

in compilers, Expression Trees are utilized which is a use of binary tree
Huffman coding trees are utilized in information pressure calculations
Priority Line is one more utilization of paired tree that is utilized for looking through greatest or least in O(1) time intricacy
Represent various leveled information
Used in altering programming like Microsoft Succeed and accounting sheets
Useful for ordering fragmented at the data set is valuable in putting away reserve in the framework
Syntax trees are utilized for most well known compilers for programming like GCC and AOCL to perform math activities
For executing need lines
Used to set aside components in less opportunity (twofold pursuit tree)
Used to empower quick memory portion in PC
Used to perform encoding and translating activity
Binary trees can be utilized to sort out and recover data from enormous datasets, like in altered record and k-d trees
Binary tree can be utilized to address the dynamic course of PC controlled characters in games, for example, in choice trees
Binary tree can be sued to carry out looking through calculations, for example, in paired search trees which can be utilized to find a component in an arranged rundown rapidly
Binary trees can be utilized to carry out arranging calculations arranging calculations, for example, in load sort which utilizes a binary heap to effectively sort component

Implementation of binary tree:

//using linked list:-

class Node {

int key;

Node left, right;

public Node(int item)

{

key = item;

left = right = null;

}

// A Java program to introduce Binary Tree

class BinaryTree {

// Root of Binary Tree

Node root;

// Constructors

BinaryTree(int key) { root = new Node(key); }

BinaryTree() { root = null; }

public static void main(String[] args)

{

BinaryTree tree = new BinaryTree();

// Create root

tree.root = new Node(1);

/* Following is the tree after above statement

/ \

null null

tree.root.left = new Node(2);

tree.root.right = new Node(3);

/* 2 and 3 become left and right children of 1

/ \

2 3

/ \ / \

null null null null */

tree.root.left.left = new Node(4);

/* 4 becomes left child of 2

/ \

2 3

/ \ / \

4 null null null

/ \

null null

}

// JAVA implementation of tree using array

//using arrays

// numbering starting from 0 to n-1.

// Importing required classes

import java.io.*;

import java.lang.*;

import java.util.*;

// Class 1

// Helper class (Node class)

public class Tree {

// Main driver method

public static void main(String[] args)

{

// Creating object of class 2 inside main() method

Array_imp obj = new Array_imp();

// Setting root node

obj.Root("A");

obj.set_Left("B", 0);

obj.set_Right("C", 0);

obj.set_Left("D", 1);

obj.set_Right("E", 1);

obj.set_Right("F", 2);

obj.print_Tree();

}

// Class 2

// Helper class

class Array_imp {

// Member variables of this class

static int root = 0;

static String[] str = new String[10];

// Method 1

// Creating root node

public void Root(String key) { str[0] = key; }

// Method 2

// Creating left son of root

public void set_Left(String key, int root)

{

int t = (root * 2) + 1;

if (str[root] == null) {

System.out.printf(

"Can't set child at %d, no parent found\n",

t);

}

else {

str[t] = key;

}

// Method 3

// Creating right son of root

public void set_Right(String key, int root)

{

int t = (root * 2) + 2;

if (str[root] == null) {

System.out.printf(

"Can't set child at %d, no parent found\n",

t);

}

else {

str[t] = key;

}

// Method 4

// To print our tree

public void print_Tree()

{

// Iterating using for loop

for (int i = 0; i < 10; i++) {

if (str[i] != null)

System.out.print(str[i]);

else

System.out.print("-");

}

Binary tree traversals:

Tree Traversal algorithms can be classified broadly into two categories:

· Depth-First Search (DFS) Algorithms

· Breadth-First Search (BFS) Algorithms

Tree Traversal using Depth-First Search (DFS) algorithm can be further classified into three categories:

· Preorder Traversal (current-left-right): Visit the current node before visiting any nodes inside the left or right subtrees. Here, the traversal is root – left child – right child. It means that the root node is traversed first then its left child and finally the right child.

· Inorder Traversal (left-current-right): Visit the current node after visiting all nodes inside the left subtree but before visiting any node within the right subtree. Here, the traversal is left child – root – right child. It means that the left child is traversed first then its root node and finally the right child.

· Postorder Traversal (left-right-current): Visit the current node after visiting all the nodes of the left and right subtrees. Here, the traversal is left child – right child – root. It means that the left child has traversed first then the right child and finally its root node.

Tree Traversal using Breadth-First Search (BFS) algorithm can be further classified into one category:

· Level Order Traversal: Visit nodes level-by-level and left-to-right fashion at the same level. Here, the traversal is level-wise. It means that the most left child has traversed first and then the other children of the same level from left to right have traversed.

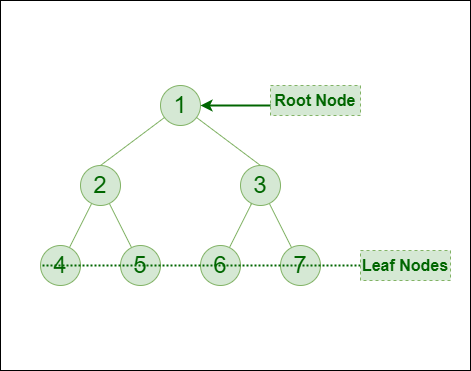Pre-order Traversal of the above tree: 1-2-4-5-3-6-7
In-order Traversal of the above tree: 4-2-5-1-6-3-7
Post-order Traversal of the above tree: 4-5-2-6-7-3-1
Level-order Traversal of the above tree: 1-2-3-4-5-6-7

Level order traversal of Binary tree in spiral form:

Follow the below steps to Implement the idea:

· Initialize a variable h to store the height of the binary tree.

· Initialize a variable i, and ltr = false.

· Traverse a loop from 1 till h:

Print the level order traversal of given traversal using below recursive function:

· printGivenLevel(tree, level, ltr)

· if tree is NULL then return;

· if level is 1, then

· print(tree->data);

· else if level greater than 1, then

· if(ltr)

· printGivenLevel(tree->left, level-1, ltr);

· printGivenLevel(tree->right, level-1, ltr);

· else

· printGivenLevel(tree->right, level-1, ltr);

· printGivenLevel(tree->left, level-1, ltr);

Update ltr = !ltr

Level order traversal of Binary tree in spiral form Using Stack:

Follow the below steps to Implement the idea:

· Initialize two stacks s1 and s2

· Push the root of tree in s1

· Initialize a while loop till either s1 or s2 is non-empty

Initialize a nested while loop till s1 contains nodes

· Initialize temp = s1.top()

· Pop the node from s1

· Print temp -> data

· If temp -> right is not NULL

· Insert temp -> right in s2

· If temp -> left is not NULL

· Insert temp -> left in s2

Initialize a nested while loop till s2 contains nodes

· Initialize temp = s2.top()

· Pop the node from s2

· Print temp -> data

· If temp -> left is not NULL

· Insert temp -> left in s1

· If temp -> right is not NULL

· Insert temp -> right in s1

Level order traversal of Binary tree in spiral form Using Deque:

Follow the below steps to Implement the idea:

· Initialize a deque dq.

· Push root of the binary tree in dq

· Initialize a variable reverse = true

· Initialize a loop while dq is not empty:

Initialize n = dq.size()
IF reverse == false:

· Initialize a nested loop while n > 0:

· Decrement n by 1

· If dq.front()->left is not NULL

· Push dq.front()->left at the back of Deque

· If dq.front()->right is not NULL

· Push dq.front()->right at the back of Deque

· Print dq.front()->key

· Pop the node from front of the Deque

· Update reverse = !reverse

Else

· Initialize a nested loop while n > 0:

· Decrement n by 1

· If dq.front()->right is not NULL

· Push dq.front()->right to the front of Deque

· If dq.front()->left is not NULL

· Push dq.front()->left to the front of Deque

· Print dq.front()->key

· Pop the node from back of the Deque

· Update reverse = !reverse

Search This Blog

binary tree

Binary tree Basics

Types of binary trees

Tree Traversal using Depth-First Search (DFS) algorithm can be further classified into three categories:

Tree Traversal using Breadth-First Search (BFS) algorithm can be further classified into one category:

Follow the below steps to Implement the idea:

Comments

Post a Comment